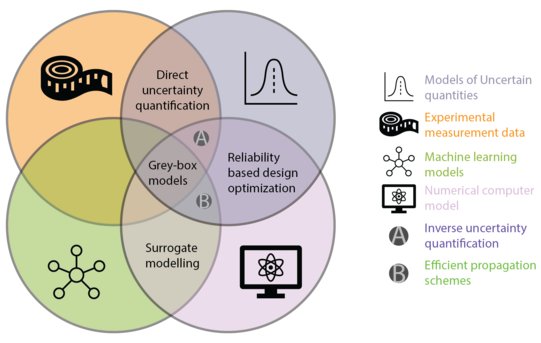
General framework
The research at the chair for Reliability Engineering aims at advancing the state-of-the-art in the field of reliability engineering on several levels, as well as bringing these approaches to engineering practice. Specifically, we perform research and provide support in the areas of:
- Modelling uncertain quantities based on experimental data
- Propagating uncertainties through expensive numerical simulation models
- Surrogate modelling schemes and machine learning approaches and their uncertainties, including grey-box models and active learning approaches
- Reliability-based and robust design optimization of components, processes or systems
While our focus is mostly aimed at problems in mechanical engineering in its widest interpretation, we are also interested in application domains from, e.g., civil engineering, biomedical engineering, geotechnical engineering or logistics.
Modelling uncertainties based on experimental data
Research at the chair is both aimed at the direct and indirect quantification of uncertainties based on experimental data. Concerning the direct identification, research is aimed at identifying random and interval field models to represent uncertainties that are spatially distributed over the model domain (e.g., mechanical properties of natural materials or parts produced using additive manufacturing). Hereto, novel, state-of-the-art probabilistic and non-probabilistic methods are being developed. Concerning the indirect identification, we develop (approximate) Bayesian computational frameworks to quantify model quantities that cannot be measured directly (e.g., clamping stiffness of a bolted connection or spatially distributed mechanical properties), based on the experimental measurement of easier-to-measure quantities (such as full-field strain measurements, or resonance frequencies). We are mostly interested in performing uncertainty modelling and characterization under the constraints of limited data.
Key papers since 2022 (preprints available for download over here):
- Faes, M., Broggi, M., Spanos, P.D., Beer, M. (2022). Elucidating appealing features of differentiable auto-correlation functions: a study on the modified exponential kernel. Probabilistic Engineering Mechanics, Vol. 69, 103287
- Bartsoen, L., Faes, M.G.R., Skipper Andersen, M., Wirix-Speetjens, R., Moens, D., Jonkers, I., Vander Sloten, J. (2023). Bayesian parameter estimation of ligament properties based on tibio-femoral kinematics during squatting. Mechanical Systems and Signal Processing, Volume 182, 1 January 2023, 109525. 10.1016/j.ymssp.2022.109525
- Behrendt, M., Faes, M., Valdebenito, M.A., Beer, M. (2023). Estimation of an imprecise power spectral density function with optimised bounds from scarce data for epistemic uncertainty quantification. Mechanical Systems and Signal Processing. Volume 189, 15 April 2023, 110072. 10.1016/j.ymssp.2022.110072
Propagating uncertainties through expensive numerical models
Research in this direction develops advanced probabilistic and imprecise probabilistic computational schemes to propagate identified uncertainties to the uncertainty on response quantities of interest. Examples of such response quantities are not only mean values and standard deviations of the responses, but also metrics for the sensitivity of the response to the input uncertainty, as well the probability that a certain value is exceeded. In this context, we develop intelligent Monte Carlo simulation schemes, as well as augmented space methods and operator norm theory with a focus on structural dynamical applications.
Key papers since 2022 (preprints available for download over here):
- Valdebenito, M., Yuan, X., Faes, M. (2023). Augmented First-Order Reliability Method for Estimating Fuzzy Failure Probabilities. Structural Safety. Accepted for publication.
- Callens, R., Faes, M., Moens, D. (2022). Multilevel Quasi-Monte Carlo For Interval Analysis. International Journal For Uncertainty Quantification, Issue 12(4). pp. 1–19. 10.1615/Int.J.UncertaintyQuantification.2022039245
- Fina, M., Lauff, C., Faes, M., Valdebenito, M., Wagner, W., Freitag. S. (2022). Bounding Imprecise Failure Probabilities in Structural Mechanics based on Maximum Standard Deviation. Structural Safety. Volume 101, March 2023, 102293 10.1016/j.strusafe.2022.102293
Surrogate modelling schemes
Concerning surrogate modelling, we mostly contribute to the development of Bayesian active learning schemes for performing highly efficient surrogate modelling of complex numerical models. The core idea here is to replace a numerical simulation model that might take minutes or hours to solve by an equally accurate surrogate model that is solved in seconds or faster. The key ingredient here is active learning, which intelligently calls the numerical model iteratively to steer the training of the surrogate model. In this context, we also have a strong focus on developing physics-informed machine learning models such as PINNs or grey-box modelling approaches.
Key papers since 2022 (preprints available for download over here):
- Dang, C., Valdebenito, M., Faes, M.G.R., Wei, P., Beer, M. (2022). Structural Reliability Analysis, a Bayesian perspective, Structural Safety, Volume 99, November 2022, 102259. 10.1016/j.strusafe.2022.102259
- Hong, F., Wei, P., Song, J., Faes, M., Valdebenito, M., Beer, M. (2023). Combining Data and Physical Models for Probabilistic Analysis: A Bayesian Augmented Space Learning Perspective. Probabilistic Engineering Mechanics. Volume 73, July 2023, 103474. 10.1016/j.probengmech.2023.103474
- Bogaerts, L., Dejans, A., Faes, M., Moens, D. (2023). A machine learning approach for efficient and robust resistance spot welding monitoring. Welding in the World. 10.1007/s40194-023-01519-1
Reliability-based and robust design optimization of components, processes or systems
In the field of reliability-based and robust design optimization, our efforts are aimed at reducing the computational cost that is associated with integrating uncertainty in design optimization problems. In essence, traditionally, one needs to propagate the uncertainties at every step of the design optimization, making the computational cost excessive to apply these methods in practical situations. At the CRE, we develop state-of-the-art methods to decouple both problems based on augmented space approaches, Markov Chain Monte Carlo simulation and operator norm theory. Further research directions also include reliability-based and robust topology optimization.
Key papers since 2022 (preprints available for download over here):
- van Mierlo, C., Persoons, A., Faes, M., Moens, D. (2023). Robust design optimization of expensive stochastic simulators under lack-of-knowledge. ASCE/ASME Journal for Risk and Uncertainty in Engineering Systems, Part B: Mechanical Engineering. Volume 9(2), 021205. 10.1115/1.4056950
- Yuan, X., Valdebenito, M.A., Zhang, B., Faes, M., Beer, M. (2023). Efficient decoupling approach for reliability-based optimization based on augmented Line Sampling and combination algorithm. Computers & Structures. Volume 280, May 2023, 107003. 10.1016/j.compstruc.2023.107003
- Van Mierlo, C., Persoons, A., Faes, M., Moens, D. (2023). Robust design optimisation under lack-of-knowledge uncertainty. Computers & Structures. Volume 275, 15 January 2023, 106910. 10.1016/j.compstruc.2022.106910







